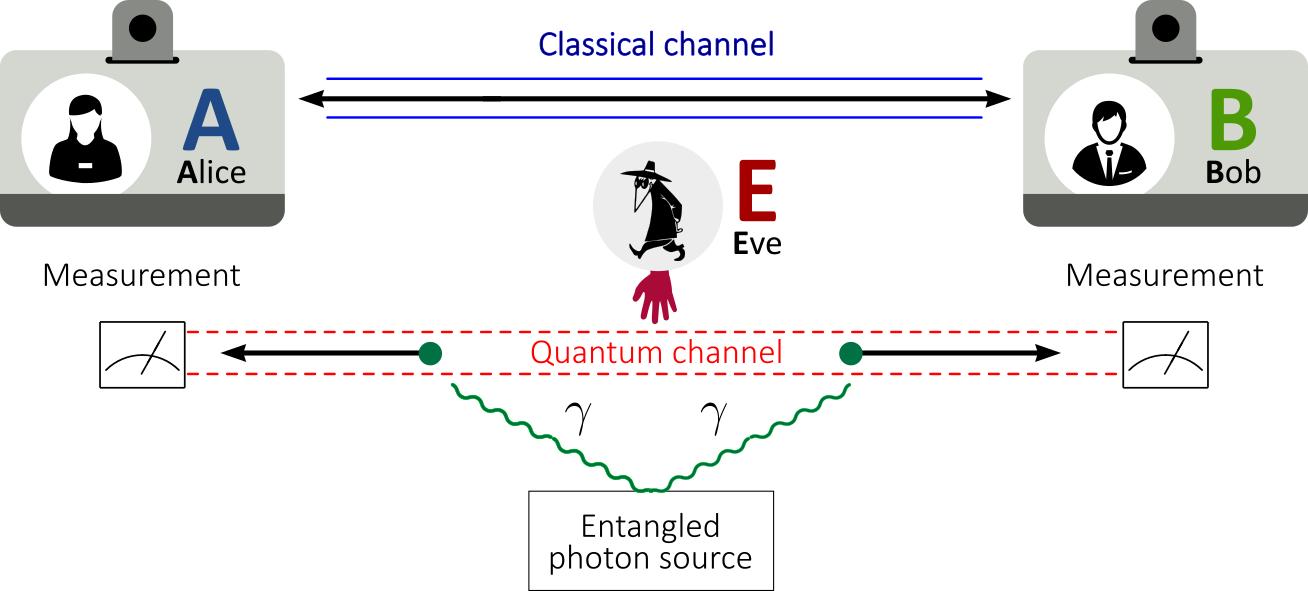
O protocolo BB84 é o primeiro modelo formal de distribuição quântica de chaves (Quantum Key Distribution – QKD), proposto em 1984 pelos cientistas Charles Bennett e Gilles Brassard, além de também ser o primeiro protocolo de fóton-único da criptografia quântica explorando diretamente a não comutatividade dos observáveis — não podem ser medidos simultaneamente com precisão; e a inviabilidade de clonagem de estados arbitrários (Teorema da não-clonagem).

A não-comutatividade dos observáveis

A transmissão de informações nesse tipo de modelo é através do envio de estados de qubits representados por fótons polarizados que são preparados pelo personagem transmissor — o qual chamaremos de Alice — em duas bases não comutativas:

• Base retilínea: autoestados de $\sigma_z$, $|0\rangle$ e $|1\rangle$.
• Base diagonal: autoestados de $\sigma_x$, $|+\rangle$ e $|-\rangle$.

A não comutatividade é expressa pela relação:

$$ [\sigma_z, \sigma_x] = 2i\sigma_y \neq 0 $$

Se o espião (vamos abordar isso mais para frente) mede numa base automaticamente ele destrói a informação sobre a outra, não há como medir simultaneamente com precisão como já mencionado, traduzindo-se no colapso (projeção) do estado quântico:

$$ |\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \ \text{Resultado: } |0\rangle \text{ (prob. } \frac{1}{2}\text{)} \ \text{ou } |1\rangle \text{ (prob. } \frac{1}{2}\text{)} $$

Um autoestado de uma base não é autoestado da outra.

Teorema da não-clonagem

Estados de bases diferentes não são ortogonais, portanto, pela existência do teorema da não-clonagem não se é possível clonar perfeitamente um estado arbitrário, significando que o invasor não pode copiar o fóton e aguardar a revelação das bases.

Seguraça do protocolo

A segurança desse esquema baseia-se em dois pilares fundamentais: a propriedade quântica de que o ganho só é possível se houver um canal clássico público autenticado — compatível com a restrição relativística da impossibilidade de comunicação superluminal; e também de que haverá perturbação do sinal caso ele seja interceptado ou tenha ruído estatisticamente relevante (quantificado pelo QBER) durante sua execução.

Essa arquitetura estabelece, portanto, um modelo em que a confidencialidade da chave não decorre de hipóteses computacionais (como dificuldade de fatoração ou de logaritmo discreto), mas sim de comportamentos fundamentais da mecânica quântica.

O protocolo

Alice prepara cada qubit da seguinte forma:

1. Seleciona aleatoriamente um bit clássico $b \in {0,1}$ e uma base $B \in {Z, X}$ com probabilidade uniforme.

2. Prepara o estado quântico $|\psi\rangle$ $$ |\psi\rangle = \begin{cases} |0\rangle & \text{se } b=0 \text{ e } B = Z, \ |1\rangle & \text{se } b=1 \text{ e } B = Z, \ |+\rangle = \dfrac{|0\rangle + |1\rangle}{\sqrt{2}} & \text{se } b=0 \text{ e } B = X, \ |-\rangle = \dfrac{|0\rangle - |1\rangle}{\sqrt{2}} & \text{se } b=1 \text{ e } B = X. \end{cases} $$

3. Assim que Bob recebe o qubit enviado por Alice, ele também escolhe aleatoriamente uma base de medição $( B' \in {Z, X} )$, com probabilidade uniforme. Ele então mede o qubit na base escolhida $( B' )$, obtendo um resultado bit $( b' \in {0,1} )$:

Seja o qubit enviado por Alice $( |\psi\rangle )$. As probabilidades de Bob obter cada resultado dependem da base escolhida:

• Caso 1: Bob escolhe a base Z $$[ \text{Prob}(b'=0) = |\langle 0 | \psi \rangle|^2, \quad \text{Prob}(b'=1) = |\langle 1 | \psi \rangle|^2 ]$$

• Caso 2: Bob escolhe a base X $$[ |+\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}}, \quad |-\rangle = \frac{|0\rangle - |1\rangle}{\sqrt{2}} ]$$ $$[ \text{Prob}(b'=0) = |\langle + | \psi \rangle|^2, \quad \text{Prob}(b'=1) = |\langle - | \psi \rangle|^2 ]$$

Agora, considerando os quatro estados possíveis enviados por Alice:

• $( |\psi\rangle = |0\rangle )$ $$[ \begin{cases} B'=Z: & \text{Prob}(b'=0)=1, \quad \text{Prob}(b'=1)=0 \ B'=X: & \text{Prob}(b'=0)=\frac{1}{2}, \quad \text{Prob}(b'=1)=\frac{1}{2} \end{cases} ]$$

• $( |\psi\rangle = |1\rangle )$ $$[ \begin{cases} B'=Z: & \text{Prob}(b'=0)=0, \quad \text{Prob}(b'=1)=1 \ B'=X: & \text{Prob}(b'=0)=\frac{1}{2}, \quad \text{Prob}(b'=1)=\frac{1}{2} \end{cases} ]$$

• $( |\psi\rangle = |+\rangle )$ $$[ \begin{cases} B'=Z: & \text{Prob}(b'=0)=\frac{1}{2}, \quad \text{Prob}(b'=1)=\frac{1}{2} \ B'=X: & \text{Prob}(b'=0)=1, \quad \text{Prob}(b'=1)=0 \end{cases} ]$$

• $( |\psi\rangle = |-\rangle )$ $$[ \begin{cases} B'=Z: & \text{Prob}(b'=0)=\frac{1}{2}, \quad \text{Prob}(b'=1)=\frac{1}{2} \ B'=X: & \text{Prob}(b'=0)=0, \quad \text{Prob}(b'=1)=1 \end{cases} ]$$

Dessa forma, todas as probabilidades de medição de Bob podem ser calculadas diretamente usando o produto interno $( \langle \phi | \psi \rangle )$ e o módulo ao quadrado.

4. Alice continua enviando os estados preparados até uma quantidade n de bits e Bob continua medindo. Após todos os qubits serem medidos, Alice e Bob comparam, através de um canal clássico, as bases que cada um utilizou. Se a base for a mesma, eles mantém o bit, caso seja diferente é um sinal de ruído ou possível interceptação de Eve.

O processo pode ser ilustrado pela tabela abaixo (considerando que Alice envia 10 estados quânticos para Bob):

Apenas bits cujas bases coincidem são mantidos; os demais podem indicar ruído. Esse processo é chamado de sifting do protocolo BB84 e a sequência de bits que sobrou é chamada de chave bruta. Pela imagem, nossa chave bruta, do exemplo, é: 010011.

Detecção de Eavesdropping (estimativa de erro)

Após a formação da chave bruta, Alice e Bob precisam verificar se não houve espionagem durante o sifting, já que Eve poderia ter interceptado algum fóton, medido seu estado e, ao reenviá-lo para Bob, introduzido erros na transmissão.

Agora, Alice e Bob escolhem um subconjunto dos bits da chave bruta e utilizam do canal clássico para verificação. Se todos (ou quase todos) baterem, é um sinal de que não houve interferência significativa, todavia se muitos bits diferirem, é provável que Eve tenha medido alguns qubits, pois a medida de um qubit em base errada altera seu estado, introduzindo erros.

Vamos a um pequeno exemplo de espionagem.

Repare que: ainda que a base coincida, a chave está corrompida, como mencionado, pela interceptação de Eve.

QBER (Quantum Bit Error Rate)

Mas, espera, a fase de sifting já não impede a interceptação de Eve? O sifting garante apenas que Alice e Bob usam bases compatíveis, mas não impede que Eve tenha interceptado e medido alguns qubits. Por isso, eles precisam comparar uma amostra da chave bruta para detectar possíveis erros causados por espionagem.

Seja $(K)$ a chave bruta de Alice e Bob com $(|K|)$ bits.
Seja (S \subseteq K) o subconjunto de bits escolhidos aleatoriamente para verificação, com $(|S| = n_{\text{amostra}})$. Denotemos os bits de Alice e Bob na amostra por $(S_A)$ e $(S_B)$.
O número de discrepâncias é:

$$[ n_{\text{erro}} = \big| { i \in S \mid S_A(i) \neq S_B(i) } \big| ]$$

A Quantum Bit Error Rate (QBER) é então:

$$[ \text{QBER} = \frac{n_{\text{erro}}}{|S|} ]$$

O critério de aborto do protocolo é:

$$[ \text{Se } \text{QBER} > e_{\text{limite}} \text{, aborta-se a sessão} ]$$

onde a literatura geralmente recomenda:

$$[ e_{\text{limite}} \sim 11% - 15% \quad \text{para BB84} ]$$

Se Alice e Bob atingem o critério então a conclusão é que pode ter ocorrido espionagem, a chave é descartada e o protocolo abortado.

Quanto maior o número de bits, maior chance de Eve ser detectada por pura consequência da Lei de Grandes Números. Agora que explicamos a detecção de Eve, vamos continuar o artigo como se não tivesse acontecido a espionagem. O subconjunto analisado por Bob e Alice é descartado da chave bruta, sobra-se a chave bruta confiável ou sifted key.

Error Correction

Mesmo sem Eve, o canal quântico pode introduzir ruído, fazendo alguns bits da sifted key divergirem entre Alice e Bob. Por isso utiliza-se protocolos como Cascade, Winnow ou códigos de correção de erros clássicos, corrigindo-se a chave. No entanto, vamos supor novamente que Eve deu a sorte de conseguir captar o mínimo de informação possível por qualquer que seja o motivo, ainda há risco de informação parcial conhecida por Eve.

Para eliminar essa informação, aplica-se uma função hash universal ou outro método de compressão:

$$[ K_{\text{final}} = \text{Hash}(K_{\text{corrigida}}) ]$$

Ao comprimir a chave, mesmo que Eve conheça parte da chave corrigida, a chave final se torna praticamente impossível de ser prevista, garantindo segurança quase perfeita. Importante lembrar que: Alice e Bob concordam previamente ou negociam no canal clássico qual função hash universal vão usar.

Chave final segura (secure key)

Finalmente, Alice e Bob tem a versão da chave que foi corrigida de erros e passou por amplificação de privacidade, garantindo que Eve tenha informação praticamente nula sobre ela, finalizando o protocolo BB84 e cumprindo seu propósito. Os próximos passos podem ser: a chave ser usada diretamente para criptografia simétrica, como One-Time Pad (OTP), ou como chave para protocolos de criptografia convencionais (AES, etc.).

Exemplo breve de One-Time Pad (OTP)

Definição: é o exemplo clássico de criptografia perfeitamente segura, desde que a chave seja igual em tamanho à mensagem que quer enviar, totalmente aleatória e usada apenas uma única vez. Alice e Bob irão utilizar a criptografia por XOR (ou exclusivo).